These are my complete notes for the various topic Introductions in Symmetric Cryptography.
I color-coded my notes according to their meaning - for a complete reference for each type of note, see here (also available in the sidebar). All of the knowledge present in these notes has been filtered through my personal explanations for them, the result of my attempts to understand and study them from my classes and online courses. In the unlikely event there are any egregious errors, contact me at jdlacabe@gmail.com.
Summary of Introductions (Symmetric Cryptography)
Table Of Contents
I. Introductions
I.I Classification & Terminology.
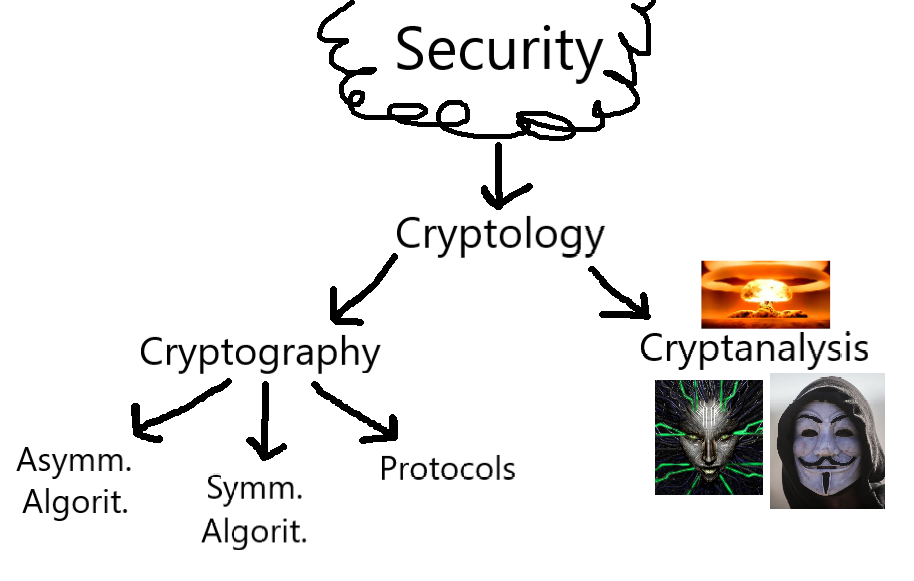
# Fig. 1. - Cybersecurity Classification Hierarchy:
# Cryptology/Cybersecurity: IT Security - the protection of digital information against misuse, incorporating technical, organizational, and implementation-specific aspects. This is the modern, digital theater of the much greater field of 'Security'.
All IT Security follows the CIA Triad: Confidentiality, Integrity and Availability of information. Security is largely focused on protecting against attackers, while system safety & reliability is focused on protecting against random technical failures.
# Cryptography: A sub-field of Cryptology;
The science of securing communication through encryption, especially against the cryptanalysis efforts of an adversary. Cryptographic algorithms are the bedrock of all cybersecurity systems - if cybersecurity is a car, then Cryptography is the engine.
# Cryptanalysis: A sub-field of Cryptology;
The reductive counterpart to Cryptography, the science of 'breaking' encryption and bypassing the cryptographic security. Though it is the medium of hackers and cybercriminals, it is also a serious scientific field for researchers to test the security of cryptosystems, i.e. systems established using Cryptography (see definition). This is the only to absolutely ensure the security of the cryptosystem - remember Schneier's Law.
# Cryptosystem: An application/implementation of a set of cryptographic algorithms (incorporating encryption, decryption, and other mechanisms).
# Symmetric Algorithms: A sub-field of Cryptography;
The classic form of Cryptography - two parties hold a secret key, enabling one party to encrypt a message and the other party to decrypt it. Thus, the same key is used for both encryption and decryption.
Until 1976, this was the only form of Cryptography in existence, and describes the basic nature of all historical ciphers (such as the shift/caesar cipher and affine cipher) and Stream Ciphers, Block Ciphers, and DES & AES. Although it is indeed the classic form of Cryptography, it is still highly relevant today, as AES remains an industry standard even into the quantum age.
Hash functions are somewhat similar to symmetric algorithms, though they can be considered an independent, third type of Cryptographic algorithm.
# Asymmetric/Public-Key Algorithms: A sub-field of Cryptography;
The great cryptographic breakthrough of the 20th century, Asymmetric Cryptography (a.k.a. "Public Key Cryptography") is the backbone of most modern cryptosystems and is what much of the infrastructure of the Internet (protocols, in particular) is based on.
Invented by the Diffie-Hellman team in 1976, Public-Key Cryptography functions by having each party have TWO keys, a private key and a public key.
For more detail on how these algorithms work, see the "Public-Key Cryptography" Subcategory ([[[[[), but know they are used in a variety of fashions: digital signatures, key establishment/management, and more!
# Protocols: A sub-field of Cryptography;
Collective cryptographic algorithms that serve a complex security function, like a library of algorithms that work together for a common goal. For example - the Transport Layer Security scheme (TLS) and the Hypertext Transfer Protocol (HTTP) are used in every web browser.
In the words of Edward Snowden, "[The Internet of Things and countless] protocols have given us the means to digitize and put online damn near everything in the world that we donβt eat, drink, wear, or dwell in."
#
C. Rule .
In Cryptography, 'Primitives', 'Ciphers', and 'Algorithms' all refer to different parts of the same process: the components of a cryptosystem at different scales, algorithms being the largest scale component and primitives being the smallest.
Primitives are the basic cryptographic functions (building blocks of an algorithm), Ciphers are the implementation of an encryption scheme, and Algorithms are the combined procedures of primitives and ciphers to create the greater cryptosystem.
For example, a well-formed algorithm may incorporate the AES cipher (see Rule [[[), which uses the key schedule primitive (see Rule [[[) to assist in both encrypting and decrypting the data.
Primitives are the basic cryptographic functions (building blocks of an algorithm), Ciphers are the implementation of an encryption scheme, and Algorithms are the combined procedures of primitives and ciphers to create the greater cryptosystem.
For example, a well-formed algorithm may incorporate the AES cipher (see Rule [[[), which uses the key schedule primitive (see Rule [[[) to assist in both encrypting and decrypting the data.
# Channel: A transmission medium for data to pass through. Examples include the Internet, airways, and Wi-Fi. Securing transmitted data from being intercepted, and from being intercepted in any meaningful form, is the goal of Cryptography.
# Hybrid Schemes: The combined usage of both asymmetric and symmetric algorithms in a cryptosystem, since both types have their own strengths and weaknesses (See [[[).
I.II Symmetric Crypto. Basics.
#
C. Rule .
Symmetric Cryptosystem:
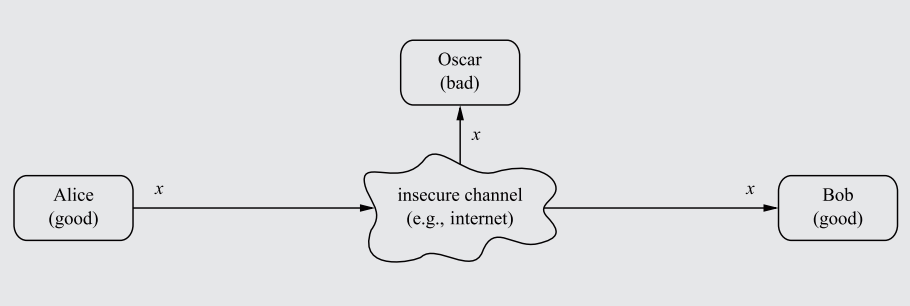
The ancient problem presents itself: How can two parties communicate over an insecure channel (an 'open channel') without having their communications intercepted by a third-party?
Say Alice and Bob connect through the internet (which is an open channel due to the potential of package rerouting/interception) and transfer data. An opponent, Oscar, can read their communications by intercepting the data before it reaches Bob.
A diagram showcasing how communications between Alice and Bob, when passing through an insecure channel unencrypted, can be intercepted by the attacker Oscar.
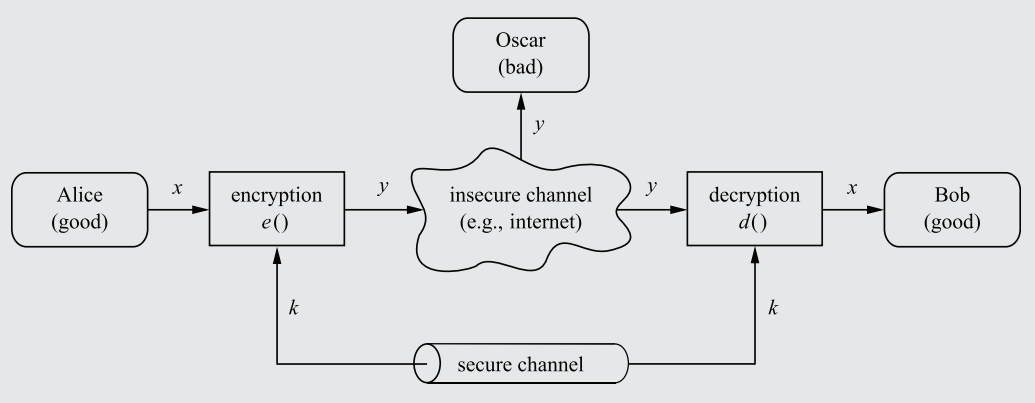
To stop Oscar from reading the message, an encryption algorithm can be established, converting the plaintext message (x) into a ciphertext message (y), and then sending it through the insecure channel. Oscar would only see a stream of random characters/bits as a result of the encryption. Bob, using a decryption function, would convert the ciphertext back into plaintext, thus completing the data transfer without interception.
In order for Bob to not simply decrypt the ciphertext immediately using the decryption function (which, counterintuitively, should actually be made publicly available - see Rule 3), a Key only known to Alice and Bob (sent through a secure, impenetrable channel) must be used as a parameter in both the encryption and decryption functions.
The key must be inputted into the encryption function to influence the manner in which the plaintext is encrypted into cyphertext. Thus, only with the key will Bob be able to decrypt the Ciphertext. Oscar, who doesn't know the key, will be unable to decrypt the message, even if the decryption algorithm is public.
A diagram showcasing a symmetric cryptosystem, complete with a key sent through a secure channel and encryption/decryption functions.
x = Plaintext message - the unadulterated, original content of the message.
y = Ciphertext, which looks like scrambled characters to an interceptor like Oscar.
e = Encryption function, a mathematical formula that converts x into y.
d = Decryption function, a mathematical formula that converts y into x.
K = The Key fed into the encryption and decryption functions.
|K|, π¦ = Keyspace, the total number of possible keys in a cryptosystem. This matters significantly with regard to brute-force Cryptanalysis (see Rule 8), and entails other characteristics detailed in Rule 6.
The ancient problem presents itself: How can two parties communicate over an insecure channel (an 'open channel') without having their communications intercepted by a third-party?
Say Alice and Bob connect through the internet (which is an open channel due to the potential of package rerouting/interception) and transfer data. An opponent, Oscar, can read their communications by intercepting the data before it reaches Bob.
To stop Oscar from reading the message, an encryption algorithm can be established, converting the plaintext message (x) into a ciphertext message (y), and then sending it through the insecure channel. Oscar would only see a stream of random characters/bits as a result of the encryption. Bob, using a decryption function, would convert the ciphertext back into plaintext, thus completing the data transfer without interception.
In order for Bob to not simply decrypt the ciphertext immediately using the decryption function (which, counterintuitively, should actually be made publicly available - see Rule 3), a Key only known to Alice and Bob (sent through a secure, impenetrable channel) must be used as a parameter in both the encryption and decryption functions.
The key must be inputted into the encryption function to influence the manner in which the plaintext is encrypted into cyphertext. Thus, only with the key will Bob be able to decrypt the Ciphertext. Oscar, who doesn't know the key, will be unable to decrypt the message, even if the decryption algorithm is public.
x = Plaintext message - the unadulterated, original content of the message.
y = Ciphertext, which looks like scrambled characters to an interceptor like Oscar.
e = Encryption function, a mathematical formula that converts x into y.
d = Decryption function, a mathematical formula that converts y into x.
K = The Key fed into the encryption and decryption functions.
|K|, π¦ = Keyspace, the total number of possible keys in a cryptosystem. This matters significantly with regard to brute-force Cryptanalysis (see Rule 8), and entails other characteristics detailed in Rule 6.
#
C. Rule .
Keeping the encryption/decryption algorithms 'e' and 'd' secret, preventing their cryptanalysis by the enemy (known as Security by Obscurity), was standard procedure for the ~4000 year history of Cryptography prior to the discovery of public-key Cryptography. However, the only way of ensuring the security of the algorithms is to make them public so that they can be analyzed by cryptanalysts.
This is the central principle of a foundational law in Cryptography, postulated in 1883 by Auguste Kerckhoffs:
Kerckhoffs' Principle:
"A cryptosystem should be secure even if the attacker (Oscar) knows all the details of the system, with the exception of the secret key."
In Practice: Never use an untested Crypto algorithm! Furthermore, never roll your own crypto!
This is the central principle of a foundational law in Cryptography, postulated in 1883 by Auguste Kerckhoffs:
Kerckhoffs' Principle:
"A cryptosystem should be secure even if the attacker (Oscar) knows all the details of the system, with the exception of the secret key."
In Practice: Never use an untested Crypto algorithm! Furthermore, never roll your own crypto!
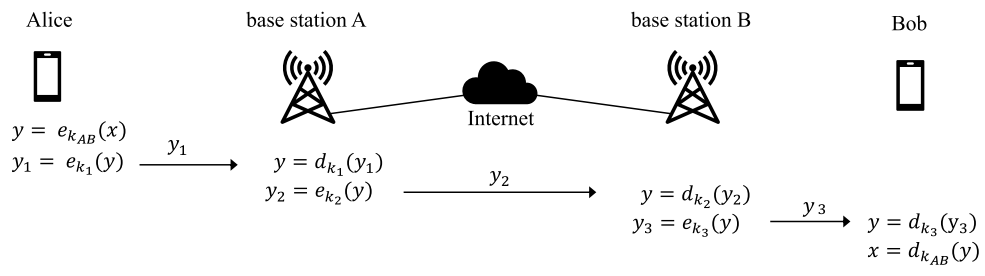
# End-To-End Encryption (E2EE): A system of encryption widely used in modern communication services (like internet messaging sites), in which all data sent from Alice to Bob (party #1 to party #2) is never decrypted at any point along its route until it reaches Bob.
Thus, all parties intercepting/eavesdropping will be unable to read or manipulate the message, even if they control any of the base stations the message goes through.
I.III Key Terminology.
Binary is a crucial element of how most (and practically all modern) cryptosystems work, and several phrases commonly used in cryptographic discussions directly reference this inherent nature. As such, let it be known: all references to 'bits' of any kind are made in regard to 1s and 0s.
#
C. Rule .
Bit-Length:
Mathematical Definition:
Value-based Bit-length = βlog2 Nβ + 1
Set-based Bit-length = βlog2 Sβ
N = Any given number.
S = Any given set.
β, β = The Floor function, which returns the greatest integer less than or equal to the given value.
β, β = The Ceiling function, which returns the smallest integer larger than or equal to the given value.
Explanation:
Bit-length is a mathematical term with two definitions and two associated equations, the application of which depends on the context of what you are trying to find the bit-length of. Apart from being able to determine when to apply either definition, bit-length is a remarkably simple concept that hinges on comprehension of binary.
The first definition is value-based, while the second is set-based.
The bit-length of a value is the # of bits required to represent a given number.
The bit-length of a set is the # of bits necessary to represent the number of values within the set.
While the value-based definition is most popular in computer science (such as in the bit_length() method in Python), the set-based definition is the most popular and relevant in Cryptography. Thus, in cryptographic discussions, it is practically always safe to assume that the term 'bit-length' is being used in regard to the set-based definition.
As such, two distinct equations emerge to represent these binary operations. As shown in the mathematical definition, the value-based bit-length uses the floor function while the set-based bit-length uses the ceiling function, rounding downward and upward for any decimal value, respectively.
For an example of the two in practice, a keyspace of 2^3 (8 values) would have a value-based bit-length of 4, since 8 is 1000 in binary, and would have a set-based bit-length of 3, since exactly 3 bits would be required to account for every value within the keyspace: 000 through 111 represent a total of 8 values, reaching a highest value of π¦-1.
With regards to set-based bit-length, this does not mean that each individual value requires three bits to represent it; the value of 1 only "requires" 1 bit to represent it, for example. The set-based bit-length only really means the total number of bits necessary to represent π¦-1, which thus accounts for all of the values before it (through the nature of binary representation).
Mathematical Definition:
Value-based Bit-length = βlog2 Nβ + 1
Set-based Bit-length = βlog2 Sβ
N = Any given number.
S = Any given set.
β, β = The Floor function, which returns the greatest integer less than or equal to the given value.
β, β = The Ceiling function, which returns the smallest integer larger than or equal to the given value.
Explanation:
Bit-length is a mathematical term with two definitions and two associated equations, the application of which depends on the context of what you are trying to find the bit-length of. Apart from being able to determine when to apply either definition, bit-length is a remarkably simple concept that hinges on comprehension of binary.
The first definition is value-based, while the second is set-based.
The bit-length of a value is the # of bits required to represent a given number.
The bit-length of a set is the # of bits necessary to represent the number of values within the set.
While the value-based definition is most popular in computer science (such as in the bit_length() method in Python), the set-based definition is the most popular and relevant in Cryptography. Thus, in cryptographic discussions, it is practically always safe to assume that the term 'bit-length' is being used in regard to the set-based definition.
As such, two distinct equations emerge to represent these binary operations. As shown in the mathematical definition, the value-based bit-length uses the floor function while the set-based bit-length uses the ceiling function, rounding downward and upward for any decimal value, respectively.
For an example of the two in practice, a keyspace of 2^3 (8 values) would have a value-based bit-length of 4, since 8 is 1000 in binary, and would have a set-based bit-length of 3, since exactly 3 bits would be required to account for every value within the keyspace: 000 through 111 represent a total of 8 values, reaching a highest value of π¦-1.
With regards to set-based bit-length, this does not mean that each individual value requires three bits to represent it; the value of 1 only "requires" 1 bit to represent it, for example. The set-based bit-length only really means the total number of bits necessary to represent π¦-1, which thus accounts for all of the values before it (through the nature of binary representation).
#
C. Rule .
Key-Length:
Mathematical Definition:
Key-length = βlog2 π¦β
π¦ = Keyspace, the total number of possible keys in a cryptosystem.
β, β = The Ceiling function, which returns the smallest integer larger than or equal to the given value.
Explanation:
Key-Length is a concept that builds upon the idea of bit-length, which is explained in Rule 4. Comprehension of bit-length (and the different between value-based and set-based bit-length) is prerequisite for understanding key-length.
In its essence, Key-length is a narrowed application of set-based bit-length specific to the bit-length of the key of a cryptosystem. It is identical in every way to the set-based bit-length definition, except for the minute change of "set" to "keyspace":
The bit-length of a keyspace is the # of bits necessary to represent the number of values within the keyspace. This value is known as the key-length.
Set-based bit-length, and its particular use-case of key-length, will appear with some ubiquity in the Cryptographic Summary. Note how key-length is basically just a subtype of bit-length, just like how keybits (see definition) are a more specific type of bit. However, they can NOT be used interchangeably, for reasons outlined below.
In Cryptography, the key-length is only relevant/existent if the cryptosystem uses binary representation, as detailed in Rule 6. The number of bits necessary to represent each value of the keyspace is meaningless if there are no 'bits' involved in the cryptosystem, as is the case for the Shift Cipher (Rule 20), which has a keyspace of 26 but no meaningful key-length. Somewhat ironically, bit-length does not require a bit-based system to have a meaningful result, as it merely denotes the process of converting a value to its binary form.
Mathematical Definition:
Key-length = βlog2 π¦β
π¦ = Keyspace, the total number of possible keys in a cryptosystem.
β, β = The Ceiling function, which returns the smallest integer larger than or equal to the given value.
Explanation:
Key-Length is a concept that builds upon the idea of bit-length, which is explained in Rule 4. Comprehension of bit-length (and the different between value-based and set-based bit-length) is prerequisite for understanding key-length.
In its essence, Key-length is a narrowed application of set-based bit-length specific to the bit-length of the key of a cryptosystem. It is identical in every way to the set-based bit-length definition, except for the minute change of "set" to "keyspace":
The bit-length of a keyspace is the # of bits necessary to represent the number of values within the keyspace. This value is known as the key-length.
Set-based bit-length, and its particular use-case of key-length, will appear with some ubiquity in the Cryptographic Summary. Note how key-length is basically just a subtype of bit-length, just like how keybits (see definition) are a more specific type of bit. However, they can NOT be used interchangeably, for reasons outlined below.
In Cryptography, the key-length is only relevant/existent if the cryptosystem uses binary representation, as detailed in Rule 6. The number of bits necessary to represent each value of the keyspace is meaningless if there are no 'bits' involved in the cryptosystem, as is the case for the Shift Cipher (Rule 20), which has a keyspace of 26 but no meaningful key-length. Somewhat ironically, bit-length does not require a bit-based system to have a meaningful result, as it merely denotes the process of converting a value to its binary form.
# Keybits: The binary bits in the key used in a cryptosystem. A key-length, for example, is composed of keybits. In Cryptography, a "256-keybit key-length" is regarded as secure against brute-force attacks (see Rule 8).
# Bits of Entropy/Key Entropy: A term frequently used in cryptography, essentially just meaning a number that represents the degree of security a cryptosystem has with respect to its keyspace. It has the equation βlog2 π¦β, where π¦ is the keyspace of a cryptosystem (the number of possible keys). For example, if a cryptosystem has 2^100 keys, then that cryptosystem has 100 bits of entropy.
It really is just a term used to flex security against brute-force attacks (Rule 8), not in reference to anything tangible other than the size of the keyspace itself - it is a self-referential term, actively disguising useful information behind additional artificial buzzwords.
It happens to share the same equation as the key-length (as detailed in Rule 6 below), but note that "bits of entropy" is not a term chained to any particular requirement and can thus be applied to any cryptosystem, while the concept of a key-length has several prerequisites that limit its usage. This is in spite of the fact that "bits of entropy" uses the word "bit" - it, like bit-length (but unlike key-length, as distinguished in Rule 5), can be reasonably applied in non-bit-based cryptosystems.
#
C. Rule .
Keyspace Mathematics:
In Symmetric Cryptography, there is an inherent relation between the keyspace of a cryptosystem (|K| or π¦), and the key-length of the key (L) that the cryptosystem uses (which is dealt with in detail in Rule 5). It is fairly simple and intuitive, but has some key caveats.
If the algorithm uses a 168-bit key, then there are 2^168 possible keys. This is because the keyspace is the number of possible values that could be represented by the bits of the key-length - a key-length of 5 would have 32 possible values, i.e. every value between 00000 and 11111. Mathematically, this is represented using either of the following equations:
π¦ = 2α΄Έ
L = βlog2 π¦β
These two equations are equivalent, with the second one derived by taking the log of both sides of the first (uncoincidentally forming the key-length equation as described in Rule 5). The ceiling function (which rounds to the closest greater number) is applied to the logarithm to ensure that the key-length is an integer. Of course, the relation only holds insofar that all keys of length L are valid and equally likely to occur, which rules out a small number of symmetric cryptosystems with selective application of their keys/keybits, like DES - see Rule [[[.
There are some limitations that narrow the applicability of this relation - in effect, it only really applies to modern symmetric cryptosystems (unless specified otherwise, like the aforementioned DES). First, all ciphers that do not explicitly have a key-length, such as those that operate on letters instead of bits (e.g., every historical cipher in Section II), do not qualify. A cipher must structure its keys in the form of binary strings with fixed lengths in order for the relation to be applicable.
As stated in its definition, the very concept of a "keybit" is dependent on the fact that the cipher is using a key made from binary bits - any ciphers that do not meet that requirement are instantly null in regards to the given relation.
For example, the Shift Cipher (see Rule 20) has a keyspace of 26, but that in no way means that the "key-length" of the cipher is log2 26 (though it will indeed have log2 26 "bits of entropy"). For non-bit cryptosystems, there is no real key-length, but these ciphers are outdated nonsense cryptography that are not to be taken seriously anyways.
Furthermore, this relation does not hold for asymmetric cryptography: There is a significant difference between symmetric keys and asymmetric keys: a 128-bit symmetric key provides roughly the same security as a 3072-bit RSA (asymmetric algorithm) key. For information as to why this is, see Rule [[[.
In Symmetric Cryptography, there is an inherent relation between the keyspace of a cryptosystem (|K| or π¦), and the key-length of the key (L) that the cryptosystem uses (which is dealt with in detail in Rule 5). It is fairly simple and intuitive, but has some key caveats.
If the algorithm uses a 168-bit key, then there are 2^168 possible keys. This is because the keyspace is the number of possible values that could be represented by the bits of the key-length - a key-length of 5 would have 32 possible values, i.e. every value between 00000 and 11111. Mathematically, this is represented using either of the following equations:
π¦ = 2α΄Έ
L = βlog2 π¦β
These two equations are equivalent, with the second one derived by taking the log of both sides of the first (uncoincidentally forming the key-length equation as described in Rule 5). The ceiling function (which rounds to the closest greater number) is applied to the logarithm to ensure that the key-length is an integer. Of course, the relation only holds insofar that all keys of length L are valid and equally likely to occur, which rules out a small number of symmetric cryptosystems with selective application of their keys/keybits, like DES - see Rule [[[.
There are some limitations that narrow the applicability of this relation - in effect, it only really applies to modern symmetric cryptosystems (unless specified otherwise, like the aforementioned DES). First, all ciphers that do not explicitly have a key-length, such as those that operate on letters instead of bits (e.g., every historical cipher in Section II), do not qualify. A cipher must structure its keys in the form of binary strings with fixed lengths in order for the relation to be applicable.
As stated in its definition, the very concept of a "keybit" is dependent on the fact that the cipher is using a key made from binary bits - any ciphers that do not meet that requirement are instantly null in regards to the given relation.
For example, the Shift Cipher (see Rule 20) has a keyspace of 26, but that in no way means that the "key-length" of the cipher is log2 26 (though it will indeed have log2 26 "bits of entropy"). For non-bit cryptosystems, there is no real key-length, but these ciphers are outdated nonsense cryptography that are not to be taken seriously anyways.
Furthermore, this relation does not hold for asymmetric cryptography: There is a significant difference between symmetric keys and asymmetric keys: a 128-bit symmetric key provides roughly the same security as a 3072-bit RSA (asymmetric algorithm) key. For information as to why this is, see Rule [[[.
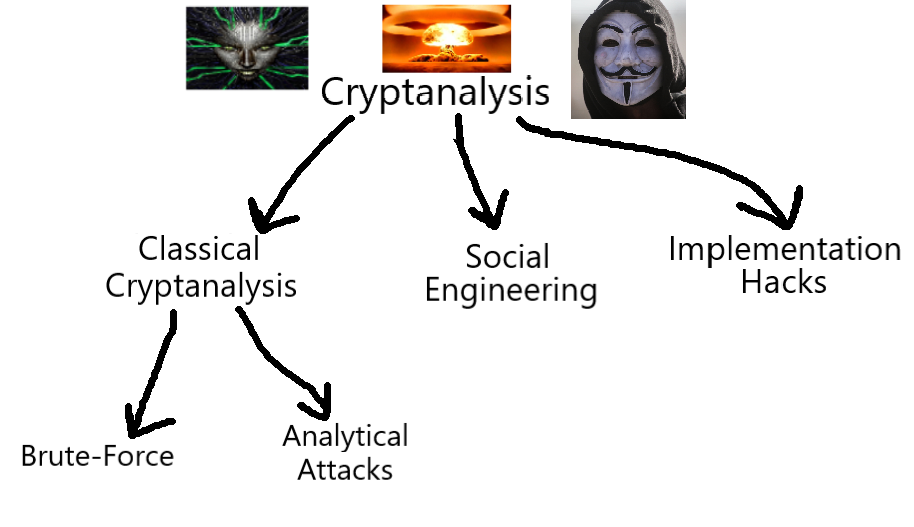
I.IV Cryptanalysis Basics.
#
C. Rule .
There are multitudes of cryptanalysis techniques, and the crucial law is that if just one attack works, then the entire cryptosystem crumbles and fails, regardless of how secure it is against other attack types.
For example, while a substitution cipher (see Rule 10) may be impenetrable to a brute-force attack (Rule 8) with its 2^88 keyspace, it collapses against letter frequency analysis (also described in Rule 10).
In order for a cryptosystem to be considered secure, it must be resistant against every single type of attack. An attacker always looks for the weakest link in the cryptosystem. Thus, in addition to strong algorithms, safeguards against social engineering and implementation attacks (see definitions below) must be instituted.
For example, while a substitution cipher (see Rule 10) may be impenetrable to a brute-force attack (Rule 8) with its 2^88 keyspace, it collapses against letter frequency analysis (also described in Rule 10).
In order for a cryptosystem to be considered secure, it must be resistant against every single type of attack. An attacker always looks for the weakest link in the cryptosystem. Thus, in addition to strong algorithms, safeguards against social engineering and implementation attacks (see definitions below) must be instituted.
# Classical Cryptanalysis: A sub-field of Cryptanalysis (see Fig. 2);
The basic, algorithm-focused approach to cryptanalysis in which you analyze the inputs and outputs to probe a viable attack vector. This is the "real" cryptanalysis in the eyes of the cryptography snobs, in which you try to poke holes in the design of the cryptosystem itself.
# Social Engineering: A sub-field of Cryptanalysis (see Fig. 2);
The process of bypassing the protections of a cryptosystem by going directly after the humans that have access to the secret key. Obtaining the key can range from kidnapping and forcing them to tell the key/password, to a simple phishing scheme over the phone or through email.
# Implementation Attacks: A sub-field of Cryptanalysis (see Fig. 2);
Extraction of the key through 'side-channel analysis'. By observing the behavior of the implementation of the cryptosystem in an IC or software, it is possible to deduce important information relating to the key.
For example: By looking at the electrical power consumption or electromagnetic radiation of a CPU running a cryptographic algorithm, a signal processing technique can be used to recover the key (see E.E. [[[[[). The runtime behavior can also indicate information regarding the key, which is why many cryptographers ensure constant runtimes in embedded cryptosystems.
These attacks are most relevant when the attacker has physical access to a piece of hardware running the cryptosystem, such as a credit card.
# Attack Vectors: The many possible ways to attack a cryptosystem; the types of cryptanalysis that can be used, including (but not limited to) those shown in Fig. 2.
# Mooreβs Law: The computing power of the strongest computers (e.g., the number of transistors in an integrated circuit) will double every 18-24 months while the price will remain constant. This means that computing power, growing exponentially over time, will continually pose more and more of a threat to modern cryptographic systems and to antiquated ones still in use, as it becomes cheaper and faster to break them.
This is especially relevant for cryptanalysis requiring intensive computing power, such as brute-force attacks (see Rule 8 below).
#
C. Rule .
Classical Attack #1: Brute-Force Attack/Exhaustive Key search:
Mathematical Definition:
Let (x, y) denote the pair of plaintext and ciphertext, and let K = {k1 ,..., kΞΊ } be the keyspace of all possible keys ki. A brute-force attack now checks for every ki β K whether dki == x.
If the equality holds, a possible correct key is found; if not, proceed with the next key.
Explanation:
The testing of all possible keys in a given keyspace with the decryption function, to find the key that will produce the plaintext. This is akin to thinking of the cryptosystem as a black box, in which the only significant factor to decoding an encrypted message is the number of possible keys the message could have been created with.
As shown in the illustration below, different keyspaces take different amounts of time to crack using brute-force. As such, only algorithms with a sufficiently large keyspace can be considered secure against brute-force, though not necessarily against any other form of attack.
A chart of the time it would take to crack keyspaces of various lengths using a brute-force attack.
As of 2010 (very recent), the largest keyspace that can be searched in a relatively reasonable amount of time is 2^60. However, not all keybits are created equally: a 128-bit symmetric key provides roughly the same security as a 3072-bit RSA (asymmetric algorithm) key, as noted in Rule 6. For why this is, see Rule [[[.
Mathematical Definition:
Let (x, y) denote the pair of plaintext and ciphertext, and let K = {k1 ,..., kΞΊ } be the keyspace of all possible keys ki. A brute-force attack now checks for every ki β K whether dki == x.
If the equality holds, a possible correct key is found; if not, proceed with the next key.
Explanation:
The testing of all possible keys in a given keyspace with the decryption function, to find the key that will produce the plaintext. This is akin to thinking of the cryptosystem as a black box, in which the only significant factor to decoding an encrypted message is the number of possible keys the message could have been created with.
As shown in the illustration below, different keyspaces take different amounts of time to crack using brute-force. As such, only algorithms with a sufficiently large keyspace can be considered secure against brute-force, though not necessarily against any other form of attack.
As of 2010 (very recent), the largest keyspace that can be searched in a relatively reasonable amount of time is 2^60. However, not all keybits are created equally: a 128-bit symmetric key provides roughly the same security as a 3072-bit RSA (asymmetric algorithm) key, as noted in Rule 6. For why this is, see Rule [[[.
#
C. Rule .
Classical Attack #2: Analytical Attacks:
The intelligent counterpart to 'brute'-force, Analytical Attacks examine the internal characteristics of the encryption function and pick apart weaknesses that could enable reconstruction of the plaintext message, such as Letter Frequency Analysis (for the Substitution Cipher, see Rule 10) and Differential Cryptanalysis (for Block and Stream Ciphers, see Rule [[[[).
There is no 'equation' for Analytical Attacks, because they are specific and unique to every cryptosystem (though some common characteristics can emerge between similar cryptosystems).
The intelligent counterpart to 'brute'-force, Analytical Attacks examine the internal characteristics of the encryption function and pick apart weaknesses that could enable reconstruction of the plaintext message, such as Letter Frequency Analysis (for the Substitution Cipher, see Rule 10) and Differential Cryptanalysis (for Block and Stream Ciphers, see Rule [[[[).
There is no 'equation' for Analytical Attacks, because they are specific and unique to every cryptosystem (though some common characteristics can emerge between similar cryptosystems).
I.V Generic Analytical Attacks.
# Ciphertext-only Attack: An attack in which the adversary only has knows the ciphertext.
# Known-plaintext Attack: In addition to the ciphertext, the adversary also knows some pieces of the plaintext (e.g., header information of an encrypted file or email).
# Chosen-plaintext Attack: An attack in which the adversary can choose the plaintext that is being encrypted and also has access to the corresponding ciphertext, found through possession of the decryption function (whether aware of its internal workings or not).
# Chosen-ciphertext Attack: An attack in which the adversary can choose ciphertexts and obtain the corresponding plaintexts, the goal being (typically) to recover the secret key.
